Poignonec Denis

Le 1 Novembre 2000

Rapport de statistique

I - Quelques rappels historiques et objectifs de cette étude_________________________ 3

A - Sir Galton régresserait-il?_______________________________________________ 3

B - Objectif de cette étude_________________________________________________ 4

II - Présentation des tableaux de données et des variables__________________________ 4

A - Présentation des tableaux de données_____________________________________ 4

B - Présentation des variables______________________________________________ 5

1 - La taille des fils________________________________________________________________ 5

2 - La taille des filles_______________________________________________________________ 5

3 - La taille des pères______________________________________________________________ 6

4 - La taille des mères______________________________________________________________ 7

III - Analyse des données pour les fils_________________________________________ 8

A - Régression multiple____________________________________________________ 8

1 - Modèle______________________________________________________________________ 8

2 - Résultats_____________________________________________________________________ 9

B - Régression simple____________________________________________________ 10

1 - Modèle_____________________________________________________________________ 10

2 - Résultats____________________________________________________________________ 10

C - Modèle empirique____________________________________________________ 11

1 - Explications__________________________________________________________________ 11

2 - Comparaison de moyennes______________________________________________________ 11

IV - Analyse des données pour les filles______________________________________ 12

A - Régression multiple___________________________________________________ 12

1 - Modèle_____________________________________________________________________ 12

2 - Résultats____________________________________________________________________ 12

B - Régression simple____________________________________________________ 13

1 - Modèle_____________________________________________________________________ 13

2 - Résultats pour la relation fille - mère________________________________________________ 13

Résultats pour la relation fille - père_____________________________________________________ 14

C - Modèle empirique____________________________________________________ 15

1 - Modèle_____________________________________________________________________ 15

2 - Résultats____________________________________________________________________ 15

V - Conclusions___________________________________________________________ 16

A - Choix des modèles___________________________________________________ 16

1 - Pour les fils__________________________________________________________________ 16

2 - Pour les filles_________________________________________________________________ 16

B - Remarques générales et critiques des modèles_____________________________ 17

1 - Remarques générales___________________________________________________________ 17

2 - Critique des données et des modèles_______________________________________________ 17

Bibliographie_____________________________________________________________ 19

Annexes__________________________________________________________________ 19

I - Quelques rappels historiques et objectifs de cette étude

A - Sir Galton régresserait-il?

En 1885, Sir Francis Galton (1822 – 1911) présenta au cours de son discours devant la chaire d'anthropologie du British Association for the Advancement of Science les résultats d'une de ses études comparant la taille adulte de 928 enfants avec celle de leurs parents (205 couples !). L'objectif de cette comparaison était d'avoir un aperçu du "pourcentage" d'héritabilité de ce caractère. Ces résultats ont été publiés en 1886 dans un article intitulé "Regression Towards Mediocrity In Heriditary Stature".

Ayant constaté que la taille des femmes était en moyenne inférieure de 8% à celle des hommes, il multiplia par 1,08 la taille des femmes pour qu'elle soit comparable à celle des hommes. Il détermina la taille du "parent – moyen", moyenne de la taille du père et de la mère, et les regroupa en 9 catégories et calcula, pour chaque catégorie, la moyenne des tailles des enfants. Par la méthode des moindres carrés, il obtient une droite d'équation : y = 26,5 + 0,611 x (NB : toutes les tailles sont en inches et 1 in = 2,54 cm), et y = 21,5 + 0,685 x, en comparant la taille des fils en fonction de celle de leurs pères.

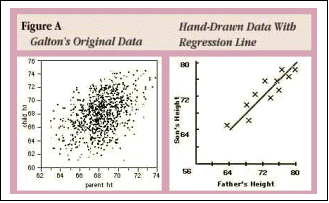
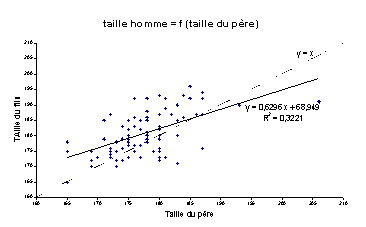
Si l'on compare ce dernier résultat avec la droite d'équation y = x (en effet on aurait tendance à dire que la taille des fils est égale à celle du père, à quelques exceptions près), on obtient le graphique suivant :

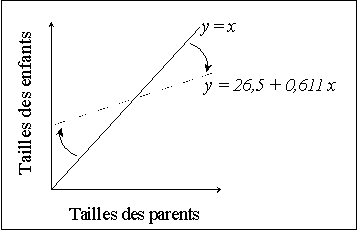
On constate alors que la taille des enfants tend à être plus modérée que celle de leurs parents. Par exemple, si les parents sont très grands, les enfants vont tendre à être grands (i.e. plus grands que la moyenne) mais plus petits que leurs parents. Inversement si les parents sont petits, les enfants vont tendre à être petits, mais plus grands que leurs parents. C'est ce que Galton a appelé : "regression towards the mean" i.e. régression vers la moyenne, avec "régression" dans le sens : "tendre vers". Plus tard ce terme de régression est resté dans le langage, mais avec un sens synonyme de celui de la méthode des moindres carrés.

Cette "régression vers la moyenne", Galton l'avait déjà remarquée lorsqu'il avait mené des études sur la taille des semences de pois (sweet peas). Il avait constaté que la taille des semences issues de semences parents de gros diamètre étaient en moyenne de gros diamètre mais de diamètre inférieur à celui des semences parents, et inversement. Selon Galton, ce phénomène de régression vers la moyenne est observable à de nombreuses reprises et est une notion assez intuitive. En effet il donne l'exemple des joueurs de football américain : le fils d'un très grand champion est moins bon que son père, même si il est supérieur à la moyenne des pratiquants. Nous reviendrons ultérieurement sur cet exemple.

B - Objectif de cette étude

L'objectif principal de cette étude est de retrouver ce principe de "régression" entre la taille des parents et celle de leurs enfants (adultes). Afin de ne pas faire une approximation de la taille des femmes (la multiplication de leur taille par 1,08 pour pouvoir la comparer à celle des hommes apparaît un peu comme empirique, même si ceci devait être fondé sur des calculs de comparaison de moyennes), nous diviserons notre étude en deux, étudiant séparément fils et filles. Nous chercherons alors à définir le meilleur modèle pour la taille des enfants, en fonction de celles de leurs parents.

Pour ce modèle, nous avons trois possibilités : expliquer la taille du fils, par exemple, par celui de son père ET de sa mère ; expliquer la taille du fils par celle de son père uniquement ; utiliser la formule empirique suivante :

Taille de l'enfant = (taille du père + taille de la mère + 10 cm)/2

II - Présentation des tableaux de données et des variables

A - Présentation des tableaux de données

N'ayant pas la possibilité d'obtenir un échantillon de grande taille (par rapport à celui de Sir Galton), l'ensemble des données proviennent du pôle ensar – insfa. Néanmoins nous supposons, a priori, que cet échantillon est assez représentatif de la population française : en effet les étudiants viennent de toutes la France, et sont âgés au minimum de 18-19 ans (croissance achevée).

Nous avons à notre disposition 3 tableaux : le premier est le tableau des données brutes, le second est le tableau où ne figurent que les fils, et le troisième tableau que les données concernant les filles. Chaque ligne du tableau contient la taille d'un individu, suivi de celle de son père et de sa mère. Toutes les tailles sont exprimées en cm.

B - Présentation des variables

Ces calculs ont été faits sur le tableau de données brutes. Notons que l'ensemble des individus regroupent des frères et des sœurs, ce qui soulèvera ultérieurement quelques problèmes.

1 - La taille des fils

Une analyse descriptive de la taille des fils donne les résultats suivants :

Analysez descriptive de la taille des fils
Moyenne	180,6136364
Erreur-type = s / Ö (n)	0,732766444
Médiane	179
Écart-type	6,873958551
Variance de l'échantillon	47,25130617
Plage	31
Minimum	165
Maximum	196
Nombre d'échantillons = n	88
Niveau de confiance (95%)	1,456453707

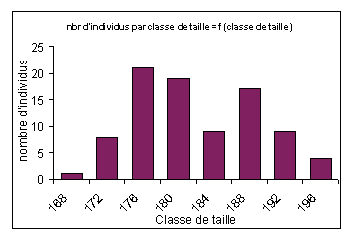
En répartissant les valeurs dans des classes, nous obtenons l'histogramme ci-dessus : nbr d'individus par classe de taille = f (classe de taille) (NB : les valeurs indiquées en abscisses sont les limites supérieures des classes).

Nous obtenons un intervalle de confiance pour la moyenne, avec un risque d'erreur de 5 % de : [179,1 ; 182,1], ce qui n'est pas très large. Au vu de notre histogramme, nous pouvons nous interroger sur la faible densité d'individus présents dans la classe [184 ; 188], ce qui aurait pu nous amener à diviser cet échantillon en 2 sous-échantillons, ou à déplacer la moyenne. A l'inverse, la classe [178 ; 180] est particulièrement bien représentée. Il aurait été intéressant de voir si ceci se retrouve avec un échantillon plus grand.

2 - La taille des filles

Une analyse descriptive de la taille des filles donne les résultats suivants :

Analyses descriptive de la taille des filles
Moyenne	166,6241135
Erreur-type = s / Ö (n)	0,53038754
Médiane	168
Écart-type	6,298003093
Variance de l'échantillon	39,66484296
Plage	33
Minimum	148
Maximum	181
Nombre d'échantillons = n	141
Niveau de confiance (95,0%)	1,048605357

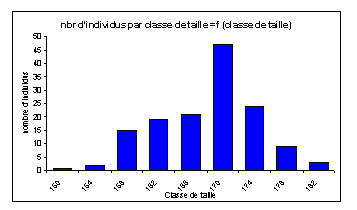
En répartissant les valeurs dans des classes, nous obtenons l'histogramme ci-dessus : nbr d'individus par classe de taille = f (classe de taille) (NB : les valeurs indiquées en abscisses sont les limites supérieures des classes).

Nous obtenons un intervalle de confiance pour la moyenne, avec un risque d'erreur de 5 %, de : [165,6 ; 167,8], ce qui est également très étroit. Notons également que l'histogramme obtenu montre une répartition beaucoup plus normale de la densité chez les filles (pas de classe creuse) que chez les fils. Ceci pourrait conforter l'hypothèse précédente, à savoir que nous n'avions pas un échantillon assez important pour les fils (141 individus pour les filles contre 88 chez les fils).

3 - La taille des pères

Deux possibilités s'offrent à nous pour décrire la taille des pères : soit nous prenons les données brutes en mélangeant fils et filles, soit nous distinguons les pères des fils et les pères des filles. Normalement, nous devrions obtenir la même moyenne.

Une analyse descriptive sur les données brutes donne les résultats suivants :

Analyse descriptive des pères
Moyenne	177,7423581
Erreur-type = s / Ö (n)	0,457531422
Médiane	177
Écart-type	6,923706772
Variance de l'échantillon	47,93771547
Plage	48
Minimum	158
Maximum	206
Nombre d'échantillons = n	229
Niveau de confiance (95,0%)	0,901531269

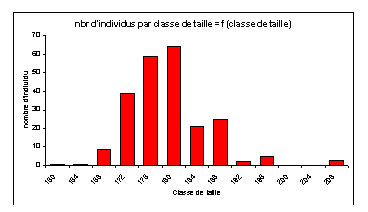
En répartissant les valeurs dans des classes, nous obtenons l'histogramme ci-dessus : nbr d'individus par classe de taille = f (classe de taille) (NB : les valeurs indiquées en abscisses sont les limites supérieures des classes).

Nous obtenons un intervalle de confiance pour la moyenne, au seuil a = 5 % de : [176,8 ; 178,6]. C'est un intervalle assez étroit. Ceci montre encore la bonne représentativité de cet échantillon, ce qui se retrouve par l'allure assez normale de l'histogramme. Nous pouvons également noter le nombre élevé d'individus présents dans les différentes classes. Ceci s'explique par le grand nombre de frères et de sœurs dans les données brutes, et donc plusieurs fois les même parents.

Comme nous avons pères = pères des fils + pères des filles, nous espérons obtenir la même moyenne, pour chacun des 3 "types" de pères. Pour les pères des fils nous obtenons un intervalle de confiance pour la moyenne m au seuil de risque a = 5 % de : [177,3 ± 1,3]. Pour les pères des filles, nous obtenons comme I.C : [178,0 ± 1,2]. Une analyse de variance à un facteur menée sur ces trois jeux de données nous donne les résultats suivants (avec : Ho = toutes les moyennes sont égales entre elles ; seuil de risque a = 5 % ; et pour les résidus E(e_ij) = 0 et V(e_ij) = s²) :

RAPPORT DÉTAILLÉ
Groupes	Nombre d'échantillons	Somme	Moyenne		Variance
père	229	40703		177,742		47,937
pèreh	88	15607		177,352		38,391
pèref	141	25096		177,985		54,056
ANALYSE DE VARIANCE
Source des variations	Somme des carrés	Degré de liberté		Moyenne des carrés		F	Probabilité	Valeur critique pour F
Entre Groupes	21,747	2		10,873		0,226	0,7973	3,0155
A l'intérieur des groupes	21837,850	455		47,995
Total	21859,598	457

Nous avons donc Proba critique (3,0) > a (0,05), ce qui nous amène à conserver Ho, i.e. à considérer les moyennes des 3 "types" de père comme égales (heureusement).

4 - La taille des mères

Comme pour les tailles des pères nous avons 3 "types" de mères : les mères des données brutes, les mères des fils et les mères des filles. De même, mères = mères des fils + mères des filles :

mère
Moyenne	163,231441
Erreur-type = s / Ö (n)	0,427425271
Médiane	163
Écart-type	6,46811804
Variance de l'échantillon	41,83655098
Plage	39
Minimum	149
Maximum	188
Nombre d'échantillons = n	229
Niveau de confiance (95,0%)	0,842209362

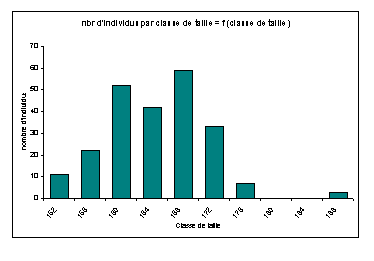
En répartissant les valeurs dans des classes, nous obtenons l'histogramme ci-dessus : nbr d'individus par classe de taille = f (classe de taille) (NB : les valeurs indiquées en abscisses sont les limites supérieures des classes).

Nous obtenons un intervalle de confiance pour la moyenne, au seuil a = 5 % de : [162,4 ; 164,1]. C'est un intervalle assez étroit, ce qui montre là encore une bonne représentativité de cet échantillon, et qui se retrouve par l'allure assez normal de l'histogramme. Nous pouvons également noter le nombre élevé d'individus présents dans les différentes classes. Ceci s'explique aussi par le grand nombre de frères et de sœurs dans les données brutes.

Comme pour les pères nous avons :

· Pour les mères des fils nous obtenons un intervalle de confiance pour la moyenne m au seuil de risque a = 5 % de : [163,5 ± 1,3].

· Pour les mères des filles, nous obtenons comme I.C : [163,0 ± 1,1].

Une analyse de variance à un facteur menée sur ces trois jeux de données nous donne les résultats suivants (avec : Ho = toutes les moyennes sont égales entre elles ; seuil de risque a = 5 % ; et pour les résidus E(e_ij) = 0 et V(e_ij) = s²) :

RAPPORT DÉTAILLÉ
Groupes	Nbre d'échantillons	Somme	Moyenne	Variance
mère	229	37380	163,231	41,836
mèreh	88	14392	163,545	39,814
mèref	141	22988	163,035	43,291
ANALYSE DE VARIANCE
Source des variations	Somme des carrés	Degré de liberté	Moyenne des carrés	F	Probabilité	P critique pour F
Entre Groupes	14,0927476	2	7,046	0,168181141	0,84525323	3,015543371
A l'intérieur des groupes	19063,3745	455	41,897
Total	19077,46725	457

Nous avons donc Probabilité critique (3,0) > a (0,05), ce qui nous amène à garder Ho, et donc à considérer les moyennes des 3 "types" de mère comme égales (heureusement).

III - Analyse des données pour les fils

Nous voulons établir un "modèle" permettant de prédire la taille du fils et d'évaluer le pourcentage de cette taille expliquée par la taille du père et / ou celle de la mère.

A - Régression multiple

Contrairement à Galton, nous avons dans un premier temps décidé d'utiliser la régression multiple car le fils est le descendant de son père et de sa mère. Nous pensons donc a priori pouvoir mieux "coller" aux données et avoir une meilleure explication de la taille du fils.

1 - Modèle

Nous voulons savoir si les variables taille du père (P) et taille de la mère (M) peuvent expliquer la taille du fils (Y).

Posons : " i Î [| 1 ; 88|], Y_i = b₀ + b₁ P_i + b₂ M_i + e_i

Avec : " i Î [| 1 ; 88|], L(e_i) = N (0, s) et " i,j Î [| 1 ; 88|]² cov(e_i ; e_j) = 0

Nous posons comme hypothèse nulle : b₀ = b₁ = b₂ = 0.

2 - Résultats

Nous obtenons les valeurs suivantes :

Statistiques de la régression
Coefficient de détermination multiple		0,571
Coefficient de détermination R^2		0,326
Erreur-type		5,707
Observations		88
ANALYSE DE VARIANCE
	Degré de liberté	SCE	CM	F	P critique de F
Régression	2	1341,654	670,827	20,590	5,10465E-08
Résidus	85	2769,209	32,578
Total	87	4110,863
	Coefficients	Erreur-type	Statistique t	Probabilité	Limite inférieure pour seuil de confiance = 95%	Limite supérieure pour seuil de confiance = 95%
Constante	61,427	20,298	3,026	0,003	21,069	101,7857822
père	0,601	0,105	5,682	1,82E-07	0,3911	0,812
mère	0,076	0,103	0,734	0,464	-0,130	0,283

Nous avons une probabilité critique de 5,1.10^-8 < a = 0,05. Nous rejetons Ho avec un risque d'erreur de 5% (ce risque est même bien plus faible puisqu'il est de 5,1.10^-8). Nous en concluons qu'il existe bien une relation linéaire entre la taille du fils, celle de son père et celle de sa mère. Le modèle peut s'écrire sous la forme

En ce qui concerne la signification des coefficients de la régression, nous voyons que si le coefficient du père ne pose pas de problème, il n'en est pas de même pour celui de la mère. En effet, si nous regardons l'intervalle de confiance de ce coefficient (pour un seuil de 5 %), la valeur 0 appartient à cet intervalle. Toutefois comme nous avons une corrélation relativement importante entre les variables taille du père et taille de la mère, nous ne pouvons pas conclure réellement sur la validité de ce coefficient.

Le coefficient de détermination (R²) nous permet de dire que 32 % de la taille du fils est explicable par le modèle, ce qui est assez raisonnable, et qui reflète bien la réalité. Nous pouvons également dire que ces 32 % expliqués par le modèle ne sont pas égaux à la somme des parts imputables au père et à la mère car il y a une corrélation de 56% entre ces deux variables. Les grands ont plutôt tendance à se marier entre eux …

Ce modèle de régression multiple ne permettant pas de déterminer le pourcentage de la taille du fils imputable au père et celle imputable à la mère, nous aurions pu réaliser une analyse de variance à 2 facteurs, mais la corrélation entre les deux variables explicatives ne nous permettra pas de différencier ces deux pourcentages.

B - Régression simple

Au vu des résultats obtenus par Galton, nous allons établir un modèle linéaire simple permettant de "prédire" la taille du fils uniquement en fonction de celle de son père.

1 - Modèle

Nous voulons savoir s’il existe une relation linéaire entre la taille du fils (Y) et celle de son père (P).

Nous posons : " i Î [| 1 ; 88|], Y_i = a + b P_i + e_i

Avec : " i Î [| 1 ; 88|], L(e_i) = N (0, s) et " i,j Î [| 1 ; 21|]² cov(e_i ; e_j) = 0

Nous posons comme hypothèse nulle : b = 0.

2 - Résultats

Nous obtenons les valeurs et le graphique suivants :

Statistiques de la régression
Coefficient de détermination multiple	0,5675
Coefficient de détermination R^2	0,3221
Erreur-type	5,6924
Observations	88

ANALYSE DE VARIANCE
	ddl	SCE	CM	F	P critique de F
Régression	1	1324,074277	1324,074277	40,86078033	8,12743E-09
Résidus	86	2786,789359	32,40452743
Total	87	4110,863636
	Coefficients	Erreur-type	Statistique t	Probabilité	Limite inférieure pour seuil de confiance = 95%	Limite supérieure pour seuil de confiance = 95%
Constante	68,9493	17,479	3,944	1,62601E-03	34,20169698	103,6968833
père	0,629	0,0984	6,392	8,12743E-09	0,433812874	0,825424964

Nous avons une probabilité critique de 8,13 . 10^-9 < a = 0.05. Nous rejetons Ho au seuil de risque de 5% (et même de 8,13 . 10^-9), ce qui signifie que nous avons bien une relation linéaire entre la taille du fils et celle du père. Nous obtenons le modèle suivant :

Dans ce modèle, nous pouvons par contre directement estimer la part explicable du père dans la taille du fils grâce au coefficient de détermination (R²), puisqu'il estime le pourcentage expliqué par le modèle (i.e. de la seule variable père). Ainsi 32 % de la taille du fils est explicable par la taille du père.

Nous avons tracé la droite d'équation y = x pour montrer que, comme Galton, nous avons des données dispersées autour de celle-ci, mais elle n'est pas le meilleur ajustement. Nous constatons aussi qu'il y une tendance des valeurs à se rapprocher de la moyenne, autrement dit, il y a une régression vers la moyenne !

C - Modèle empirique

1 - Explications

Formule que certains médecins utilisaient pour déterminer la taille adulte de l'enfant, ils sommaient la taille de ses parents à laquelle il ajoutait 10 cm et divisait le tout par 2.

Afin de voir la validité de ce modèle, nous allons calculer les tailles théoriques des fils à partir de celles de leurs parents et nous effectuerons une comparaison de moyennes entre les données obtenues et les données théoriques.

2 - Comparaison de moyennes

a) Modèle

Nous voulons savoir s’il existe une différence entre la moyenne observée de la taille des fils (Y) et la moyenne théorique (Yt).

Nous posons comme hypothèse nulle : m(Y) – m(Yt) = m1 – m2 = 0

Soit D = y1 – y2, nous posons comme statistique de test sous Ho : T = D / s_D, avec s_D = (1/88 . (s²₁ + s²₂))^^1/2.

La loi de T sous Ho est une loi de Student. A priori, nous considérons les variances de ces deux échantillons comme inégales.

b) Résultats

Nous obtenons les valeurs suivantes :

	Taille	Théorique
Moyenne	180,613	175,448
Variance	47,251	26,592
Observations	88	88
Différence hypothétique des moyennes	0
Degré de liberté	161
Statistique t	5,638
P(T<=t) unilatéral	3,767E-08
Valeur critique de t (unilatéral)	1,6546
P(T<=t) bilatéral	7,534E-08
Valeur critique de t (bilatéral)	1,974

Nous avons une Probabilité critique de 7,5 . 10^-8 < Seuil de risque de 0,05. Nous rejetons par conséquent l'hypothèse nulle au seuil de risque de 5% (ici encore, ce seuil est plus précisément de 7,5 . 10^-8). Ceci signifie donc que les deux moyennes sont différentes, et que ce modèle théorique ne peut s'utiliser pour prédire la taille des fils. Nous pouvons également noter qu'au vu de la valeur de la probabilité unilatérale, ce test à une tendance à sous-estimer la taille des fils.

Ce modèle n'étant pas valable, il est inutile de chercher à déterminer la part du père et celle de la mère dans la taille du fils dans ce modèle.

IV - Analyse des données pour les filles

Nous voulons établir un modèle permettant de "prédire" la taille de la fille et d'évaluer le pourcentage de cette taille expliquée par la taille du père et / ou celle de la mère.

Nous allons suivre la même démarche que pour les fils.

A - Régression multiple

1 - Modèle

Nous voulons savoir si les variables taille du père (P) et taille de la mère (M) peuvent expliquer la taille de la fille (Y).

Posons : " i Î [| 1 ; 141|], Y_i = b₀ + b₁ P_i + b₂ M_i + e_i

Avec : " i Î [| 1 ; 141|], L(e_i) = N (0, s) et " i,j Î [| 1 ; 88|]² cov(e_i ; e_j) = 0

Nous posons comme hypothèse nulle : b₀ = b₁ = b₂ = 0.

2 - Résultats

Nous obtenons les valeurs suivantes :

Statistiques de la régression
Coefficient de détermination multiple			0,446
Coefficient de détermination R^2			0,199
Erreur-type			5,677
Observations			141
ANALYSE DE VARIANCE
	Degré de liberté	SCE		CM	F	Proba critique de F
Régression	2	1105,526		552,763	17,151	2,225E-07
Résidus	138	4447,552		32,2286
Total	140	5553,078
	Coefficients	Erreur-type		Statistique t	Probabilité	Limite inférieure pour seuil de confiance = 95%	Limite supérieure pour seuil de confiance = 95%
Constante	86,380	13,730		6,2918	3,895E-09	59,231	113,529
père	0,194	0,073		2,638	9,274E-03	0,0488	0,3407
mère	0,279	0,082		3,388	9,161-04	0,116	0,4426

Nous avons une probabilité critique de 2,2.10^-7 < a = 0,05. Nous rejetons Ho avec un risque d'erreur de 5% (ce risque est même bien plus faible puisqu'il est de 2,2.10^-7). Nous en concluons qu'il existe bien une relation linéaire entre la taille de la fille, celle de son père et celle de sa mère. Le modèle peut s'écrire sous la forme

En ce qui concerne la signification des coefficients de la régression, nous voyons que la valeur 0 n'appartient pas aux intervalles de confiance (au seuil de risque de 5%). En comparaison avec la régression multiple chez les fils, c'est le coefficient de la mère qui devient plus important que celui du père, même si celui-ci n'est pas du tout négligeable. Ceci ce conçoit facilement puisque d'une manière générale, on serait tenté de dire : les pères influent sur les fils, et les mères sur les filles. Néanmoins nous devons tempérer ces résultats puisque ici aussi il y a corrélation entre les variables taille du père et taille de la mère.

Le coefficient de détermination (R²) nous permet de dire que 20 % de la taille de la fille est explicable par le modèle, ce qui est assez raisonnable. Comme pour les fils nous pouvons également dire que ces 20 % expliqués par le modèle ne sont pas égaux à la somme des parts imputables au père et à la mère.

Nous voyons que ce modèle de régression multiple ne permet pas de déterminer le pourcentage de la taille de la fille explicable par le père et celle explicable par la mère. Pour pouvoir les estimer, nous aurions pu réaliser une analyse de variance à 2 facteurs, mais là encore, la corrélation entre les deux variables ne nous permettrait pas de différencier les deux pourcentages.

B - Régression simple

Comme précédemment, nous allons chercher à établir une relation entre la taille de la fille et celle de la mère, mais au vu du coefficient du père, nous chercherons également à établir une relation fille - père.

1 - Modèle

Nous voulons savoir s’il existe une relation linéaire entre la taille de la fille (Y) et celle de sa mère (M) ou de son père (P)

Nous posons : " i Î [| 1 ; 141|], Y_i = a + b M_i (P_i) + e_i

Avec : " i Î [| 1 ; 141|], L(e_i) = N (0, s) et " i,j Î [| 1 ; 21|]² cov(e_i ; e_j) = 0

Nous posons comme hypothèse nulle : b = 0.

2 - Résultats pour la relation fille - mère

Nous obtenons les valeurs et le graphique suivants :

Statistiques de la régression
Coefficient de détermination multiple			0,398
Coefficient de détermination R^2			0,1584
Erreur-type			5,797
Observations			141
ANALYSE DE VARIANCE
	ddl	SCE		CM	F	Proba critique de F
Régression	1	881,095		881,095	26,214	9,991E-078E-07
Résidus	139	4671,98		33,611
Total	140	5553,078
	Coefficients	Erreur-type		Statistique t	Probabilité	Limite inférieure pour seuil de confiance = 95%	Limite supérieure pour seuil de confiance = 95%
Constante	104,461	12,150		8,596	1,527E-14	80,43711603	128,486308
mère	0,3812	0,0744		5,119	9,99E-07	0,234042381	0,528520574

Nous avons une probabilité critique de 9,99 . 10^-7 < a = 0.05. Nous rejetons Ho au seuil de risque de 5% (et même de 9,99 . 10^-7), ce qui signifie que nous avons bien une relation linéaire entre la taille de la fille et celle de la mère. Nous obtenons le modèle suivant :

Dans ce modèle, nous pouvons directement estimer la part de la mère dans la taille de sa fille grâce au coefficient de détermination (R²), puisqu'il estime la part expliquée par le modèle (i.e. de la seule variable mère). Ainsi 16 % de la taille de la fille est explicable par la taille de sa mère.

Nous avons tracé la droite d'équation y = x pour montrer que, comme pour les fils, nous avons des données dispersées autour de celle-ci et qu'il y à aussi une tendance des valeurs à se rapprocher de la moyenne, autrement dit, une régression vers la moyenne !

3 - Résultats pour la relation fille - père

Nous obtenons les résultats et le graphique suivants :

Statistiques de la régression
Coefficient de détermination multiple	0,363
Coefficient de détermination R^2	0,132
Erreur-type	5,887
Observations	141

ANALYSE DE VARIANCE
	ddl	SCE	CM	F	Valeur critique de F
Régression	1	735,474	735,474	21,220	9,162E-06
Résidus	139	4817,603	34,659
Total	140	5553,078
	Coefficients	Erreur-type	Statistique t	Probabilité	Limite inférieure pour seuil de confiance = 95%	Limite supérieure pour seuil de confiance = 95%
Constante	111,138	12,055	9,219	4,298E-16	87,303	134,973
père	0,3117	0,0676	4,606	9,169E-06	0,177	0,445

Nous avons une probabilité critique de 9,16 . 10^-6 < a = 0.05. Nous rejetons Ho au seuil de risque de 5% (et même de 9,16 . 10^-6), ce qui signifie que nous avons bien une relation linéaire entre la taille de la fille et celle du père. Nous obtenons le modèle suivant :

Dans ce modèle, nous pouvons directement estimer la part du père dans la taille de sa fille grâce au coefficient de détermination (R²), puisqu'il estime la part expliquée par le modèle (i.e. de la seule variable père). Ainsi 13 % de la taille de la fille est explicable par la taille de son père.

Nous avons tracé la droite d'équation y = x pour montrer que, comme précédemment, nous avons des données "dispersées" (cf. remarque) autour de celle-ci et qu'il y à aussi une tendance des valeurs à se rapprocher de la moyenne, autrement dit, une régression vers la moyenne !

Remarque : nous constatons un phénomène présent sur tous les graphiques de régression simple : les données sont en "colonnes". Ici ce phénomène est beaucoup plus accentué. Nous reviendrons ultérieurement sur ce point.

C - Modèle empirique

1 - Modèle

Nous voulons savoir s’il existe une différence entre la moyenne observée de la taille des filles (Y) et la moyenne théorique (Yt).

Nous posons comme hypothèse nulle : m(Y) – m(Yt) = m1 – m2 = 0

Soit D = y1 – y2, nous posons comme statistique de test sous Ho : T = D / s_D, avec s_D = (1/141 (s²₁ + s²₂))^^1/2.

La loi de T sous Ho est une loi de Student. A priori, nous considérons les variances de ces deux échantillons comme inégales.

2 - Résultats

Nous obtenons les valeurs suivantes :

	Taille	théorique
Moyenne	166,624	175,510
Variance	39,664	35,644
Observations	141	141
Différence hypothétique des moyennes	0
Degré de liberté	279
Statistique t	-12,159
P(T<=t) unilatéral	6,963E-28
Valeur critique de t (unilatéral)	1,650
P(T<=t) bilatéral	1,392E-27
Valeur critique de t (bilatéral)	1,968

Nous avons une Probabilité critique de 1,4 . 10^-27 < Seuil de risque de 0,05. Nous rejetons par conséquent l'hypothèse nulle au seuil de risque de 5% (ici encore, ce seuil est plus précisément de 1,4 . 10^-27). Ceci signifie donc que les deux moyennes sont différentes, et que ce modèle théorique ne peut s'utiliser pour déterminer la taille des filles. Nous pouvons également noter que ce test à une tendance à surestimer la taille des filles (l'inverse des fils).

Ce modèle n'étant pas valable, il est inutile de chercher à déterminer la part du père et celle de la mère dans la taille du fils dans ce modèle.

V - Conclusions

A - Choix des modèles

1 - Pour les fils

Nous rejetons d'abord le modèle empirique, qui ne donne pas de résultats satisfaisants.

Le choix de modèle issu de la régression multiple ou simple peut se faire selon plusieurs critères : le coefficient de détermination ou la probabilité critique du test de signification du modèle.

Le coefficient de détermination ne peut être un critère de sélection du modèle, car il détermine l'ajustement du modèle aux données. Or plus nous rajoutons de variables, et plus nous allons "coller" aux données. Par conséquent, le modèle issu de la régression multiple à naturellement un R² supérieur à celui de la régression simple (32,6 % contre 32,2 %); Toutefois cet écart est très minime, ce qui pourrait s'expliquer par le coefficient de la mère proche de 0 dans la régression multiple.

La valeur de la probabilité critique va nous permettre de départager ces deux modèles : P_modèle1 = 5,1 . 10^-8 et P_modèle2 = 8,1 . 10^-9. Par conséquent nous avons plus de risques de rejeter Ho avec le modèle 1 qu'avec le modèle 2 puisque P_modèle1 > P_modèle2. Nous décidons donc de garder le modèle 2 :

2 - Pour les filles

Ici également, nous rejetons le modèle empirique, qui ne donne pas de résultats satisfaisants.

En ce qui concerne le choix des 3 modèles de régressions nous allons utiliser comme précédemment, la valeur de la Probabilité critique des tests de validité des modèles : P_modèle1 = 2,2.10^-7, P_fille-mère = 9,99 . 10^-7, et P_fille-père = 9,16 . 10^-6.

Nous avons P_fille-père > P_fille-mère > P_modèle1. L'erreur de première espèce la plus petite (rejet de Ho) est donc celle du modèle issu de la régression linéaire multiple, que décidons de garder.

B - Remarques générales et critiques des modèles

1 - Remarques générales

A chaque régression linéaire, la pente de la courbe de régression obtenue était inférieure à 1. Nous retrouvons ici le résultat de Galton. Celui-ci est valable sur plusieurs jeux de données (pour les fils et pour les filles). Dans chaque cas, nous observons que les parents grands ont des enfants plus grands que la moyenne, mais moins grand qu'eux d'une manière générale, et que des parents petits ont des enfants petits par rapport à la moyenne mais plus grand qu'eux. Nous avons bien cette regression towards the mean, décrite par Galton.

Toutefois, si nous prenons le cas des hommes, une partie seulement de la taille du fils est effectivement explicable par la génétique. De nombreux autres facteurs interviennent dans le déterminisme de la taille, comme le sport, l'alimentation ainsi que de nombreux autres facteurs dits environnementaux. Notons que Galton a défini la part de l'hérédité dans son modèle comme égale au coefficient de détermination. Ceci apparaît aujourd'hui comme erroné. Le coefficient de détermination pourrait définir la part "observée" de l'héritabilité du facteur taille (ce qui va donc être utile dans des centres de sélection animal par exemple). La part réelle est beaucoup plus difficile à calculer, voir impossible. En effet, dans le système de régulation des gènes il y a de nombreux facteurs dits inhenceurs ou répresseurs, qui respectivement vont favoriser ou inhiber l'expression d'un gène.

Un autre point sur lequel nous voudrions revenir, est l'exemple donné par Galton sur les joueurs de football (américain). Nous ne sommes pas convaincus que le fils d'un excellent joueur de football soit meilleur joueur de football que la moyenne, mais moins bon que son père. D'une part, l'héritabilité de ce genre de caractère ne semble pas avéré. D'autre part cette définition pourrait alors se transposer à d'autre domaine comme celui de l'intelligence, où l'on pressent plus fortement la notion d'hérédité ; mais Einstein ne serait-t-il pas un contre exemple ? Galton nous aurait très certainement répondu qu'il s'agit d'un point extrême, un de ces points qui font justement tendre les courbes de régression vers la moyenne. Toutefois, en ce qui concerne l'intelligence, ce genre de relation n'est toujours pas admise par la communauté scientifique. Pour ce qui est du football, à voir …

2 - Critique des données et des modèles

* La première critique est celle que l'on vient de faire sur la justesse de tels modèles compte tenu du nombre de facteurs pouvant intervenir dans la taille d'un individu.

* De plus, pouvons nous considérer ces résultats comme valables par rapport au jeu de données initiales ?

· Nous ne disposions pas d'un échantillon très important pour les fils : en effet l'analyse de l'histogramme nous montre de nombreuses classes creuses. De plus la moyenne obtenue est relativement élevée. Nous pouvons aussi nous interroger sur la représentativité des différents échantillons (les personnes du pôle ensa-insa sont – elles vraiment représentatives de la population française ?)

· Bien que nous disposions d'un échantillon plus important pour les filles, les modèles obtenus présentent des défauts. Lors de la représentation graphique des régressions simples, nous avons constaté une phénomène de "colonnes", i.e. pour une taille donnée du père, par exemple, nous avons plusieurs tailles de filles. Or par définition, nous considérons la taille comme une variable continue. Nous aurions du obtenir des nuages de points beaucoup plus dispersés. Ceci pourrait s'expliquer par le fait que la récolte des données s'est faite par questionnaire et non par mesure directe. Bon nombre de personnes ont du donner leur taille de manière juste et précise, mais faire une approximation de celles de leurs parents. Ainsi, d'une mère mesurant 164 ou 166 cm, on est passé à une mère mesurant 165, valeur ronde. Enfin, une autre explication de ce phénomène pourrait être le fait que nous ayons pris en compte des frères et des sœurs, où pour des mêmes tailles de parents, nous avons plusieurs tailles d'enfants. Mais le fait que ce phénomène soit principalement marqué chez les filles tendrait à dire que les familles française à plusieurs enfants ont principalement des filles. A vérifier …

* Nous devons également nous interroger sur l'intérêt pratique de tels modèles. En effet, les personnes qui les utiliseraient le plus souvent seraient sans aucun doute les médecins. Or les deux modèles choisis impliqueraient que les médecins connaissent les formules ou utilisent des abaques, et le résultat ne serait de toute façon qu'une approximation. Il faut considérer le rapport utilité / pratique.

* Enfin, la critique qui pourrait être faite au modèle empirique, est son fondement scientifique. En effet ce modèle est applicable aussi bien pour les fils que pour les filles, ce qui signifierait qu'à l'échelle de la population, les hommes et les femmes aient la même taille. Or ceci est faux. De plus l'utilisation de ce modèle impliquerait que la taille augmenterait de façon continue de 5 cm d'une génération à l'autre. Si l'on considère que 25 ans séparent deux générations, la taille moyenne de la population devrait alors augmenter de 20 cm par siècle, et donc si nous étions des micro-lilliputiens en l'an 0, nous devrions en l'an 2000 mesurer 40 petits mètres et certainement beaucoup aimer la soupe …

Bibliographie

· Statistique, Thomas H. et Ronald J., 1990,ième édition, economica

· Why is it called regression, Ann Lehman and John Sall (SAS institute Inc.)

http://www.jmpdiscovery.com/news/jmpercable/summer98/regression.html

· Do statistics test scores regress towards the mean ?, Gary Smith (Pomona College)

http://gsmith.pomona.edu/SmithRegress.html

· Toute la bibliographie de Galton

http://www.mugu.com/galton/bibliography/full-bibliography.html#1880

· Extrait de : Regression Towards Mediocrity in Hereditary Stature, Galton, 1886, jounal of the Anthropological Institute, vol 15, 246 – 263

http://www.stat.ucla.edu/history/regression.gif

Annexes